从零开始的软渲染生活-第二话

第二话-三角形光栅化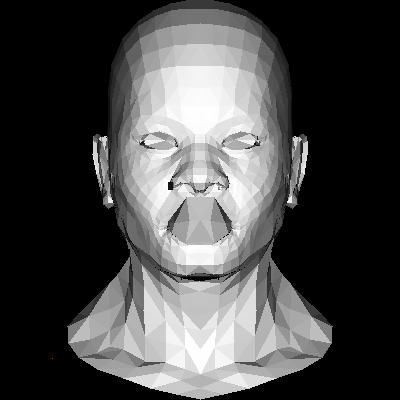
效果图
前情提要：我们已经能够通过画线来用线框表示模型了，但是完整的模型是由面片构成的，也就是说我们这次要来给三角形填色。

从这里开始我的做法就和原作者分道扬镳了，原作者也是多次强调不要一味按照他的思路来而是自己尝试，所以如果你想看原作者的思路请传送到这里

三角形的光栅化算法是非常多的，最最本质的一种就是扫描线法，即一行一行扫过去，看看哪一些点落在三角形范围内，判断点是否在三角形内部的方法也有很多，什么内角和啦，什么算面积啦，什么向量内积啦云云。

这里原作者用了Barycentric Coordinates算法，即“重心坐标系插值算法”，本质是通过计算2D空间中任意一点到三角形三边的相对距离，来确定点是否在三角形内部。推导起来并不是很直观，所以我选择另一种edge equation算法，CMU图形学课用的也是这一种。下面细说一下。

这个算法很好理解，对于三角形每一条边，我们都可以得到它的直线公式Ax+By+C=0，其中A=Y2-Y1，B=X1-X2，C=X2Y1-X1Y2。因为一条直线是把整个平面一分为二的，所以我们把每一个待判断的点代入这个公式的时候，除了落在直线上的情况有Ax+By+C=0，其它的不是大于0就是小于0，那我们又要怎么根据这个来判断呢？

其实只需要我们把三角形的第三个顶点（即不在此边上的那个点）待入这个直线方程，那么只要我们的结果都大于0或都小于0，则说明当前点与第三顶点位于直线的同一侧（称为内侧吧），那么只要对于三条边点都在内侧，那这个点就落在三角形内了，我们就可以给他上色。

之前讲图形学重在优化，所以这里我们可以采取bounding box的思想，来减少遍历的点的数量，也就是在一个刚好包裹住三角形的框进行遍历就可以了。

道理就是这么个道理，上代码：

bool edge_equation(int x0,int y0,int x1,int y1,int x2,int y2, int cur_x, int cur_y){
    int eq_cur = (y2-y1)*cur_x + (x1-x2)*cur_y + (x2*y1 - x1*y2);
    int eq_another = (y2-y1)*x0 + (x1-x2)*y0 + (x2*y1 - x1*y2);
    // if(eq_cur*eq_another>=0) return true;
    // else return false; 
    if(eq_cur>=0 && eq_another>=0)return true;
    if(eq_cur<=0 && eq_another<=0)return true;
    return false;
}

void triangle(int x0,int y0,int x1,int y1,int x2,int y2,TGAImage &image,TGAColor color,int width,int height){
    // find bounding box of the triangle
    int bb_top = y0 > y1 ? (y0 > y2 ? y0 : y2) : (y1 > y2 ? y1 : y2) +1;
    int bb_bottom = y0 < y1 ? (y0 < y2 ? y0 : y2) : (y1 < y2 ? y1 : y2) -1;
    int bb_right = x0 > x1 ? (x0 > x2 ? x0 : x2) : (x1 > x2 ? x1 : x2) +1;
    int bb_left = x0 < x1 ? (x0 < x2 ? x0 : x2) : (x1 < x2 ? x1 : x2) -1;
    for(int i=bb_left; i<=bb_right; i++){
        for(int j=bb_bottom; j<=bb_top; j++){
            if(edge_equation(x0,y0,x1,y1,x2,y2,i,j) && 
               edge_equation(x1,y1,x2,y2,x0,y0,i,j) &&
               edge_equation(x2,y2,x1,y1,x0,y0,i,j)){
                //std::cout<<i<<" "<<j<<std::endl;
                image.set(i, j, color);
            }
        }
    }
}

但是就是这么一个不算难的算法，卡了我一个晚上，怎么跑都跑不出想要的效果，为什么？

因为我一开始判断两数同符号用的是这样的方法：

1 2	// if(eq_cur*eq_another>=0) return true; // else return false;

看起来合情合理没有问题吼，但是尼玛的我忘了一件事就是，

当eq_cur和eq_another的值比较大的时候，乘起来的值就会变得超大，超过了int表示上限。。

被自己蠢！哭！了！

终于我们可以给前面的mesh网格上色填充了

接下来就可以加上光照了

光照简单来算的话就是计算每个面的法向量与光线向量的点积，我们知道点积在几何上表征着两个向量的夹角，也就是说，当光线与平面的法向量夹角越小，光照效果就越亮，那么计算平面的法向量我们可以用三角形两条边的叉积。

于是乎，悲剧地重构代码。。因为涉及了向量运算之后，得修改一下数据结构方便计算。

1 2	Vec3f light(0.,0.,-1.); float intensity = n*light;

定义光线向量，算出法向量，点乘得到一个系数，把这个系数作为颜色的参数，这里大多都是简单的数学计算了，不再细述

1	fill_triangle(x0,y0,x1,y1,x2,y2,image,TGAColor(intensity255, intensity255, intensity*255, 255));

这样就可以画出比较像样的结果了

但是嘴部还是有点问题，因为我们还没有做背面剔除

つづく