从零开始的软渲染生活-第三话

第三话-深度缓存

前情提要：前面的绘制中我们没有考虑各个面片之间的深度关系，这就导致后面画的面会直接覆盖前面画好的面，无论实际空间上哪个面是在前面的，通常我们管这叫画家算法或者优先填充。这在绘制3维物体时会有很多问题，所以这一话我们要来解决它。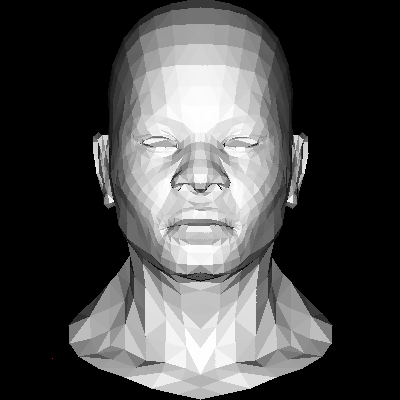

讲道理这一话知识点还是蛮多的。

首先我们要引入的一个概念就是深度缓存（z-buffer），就是我们先初始化一个画布大小的二维矩阵，里面的值初始化为负无穷，然后绘制的过程中，我们用对应位置上点的深度信息来更新这个z-buffer，如果深度值大于当前z-buffer中存储的深度，也即离观察者更近，那么我们就画出这个点，并更新深度缓存，如果小于就忽略这个点的绘制。

那么第二个要解决的问题就是怎么计算三角面上每个点的深度值，因为初始我们只能从obj文件中获得每个顶点的z值。这里要用到的就是二维平面上的一个插值算法，我们知道直线可以用线性插值，那三维面呢？

终究还是逃不离前面提到的Barycentric Coordinates算法，也就是重心坐标插值法。简单来说，三角形内一点P可以把三角形分割为三个子三角形，这三个子三角形与大三角形的面积比，即三个顶点对P点的值贡献的权值。具体表现在公式上就是：

设2D空间中，三角形三个顶点分别为A,B,C，则任意一点P均可表示为P = A + u(B-A) + v(C-A)，展开得P = (1 - u - v) * P1 + u * P2 + v * P3，现在我们有各个顶点的信息，同时只有两个未知数，那么问题就变成了求解二元一次方程组。

P.x = (1 - u - v) * P1.x + u * P2.x + v * P3.x

P.y = (1 - u - v) * P1.y + u * P2.y + v * P3.y

求出u，v我们就可以计算平面上任意一点的深度值。

又，P = A + u(B-A) + v(C-A)即表示PA向量其实可以由AB和AC加权得到。所以可以推出：

uAB + vAC + PA = 0

这样一来我们求解方程组就方便多了，因为我们直接就可以用向量的叉积！

不过还有一个问题就是，当前计算的深度值并非正确的，因为三维空间投影到二维上，z值不是线性变化的，实际上，透视矫正之后应该是P.y/P.z = (1 - u - v) * P1.y/P.z + u * P2.y/P.z + v * P3.y/P.z

之后对三个点的深度值加权平均就可以了。

Vec3f barycentric(Vec3f A, Vec3f B, Vec3f C, Vec3f P) {
    //Vec3f s[2];
    Vec3f eq_x(C.x-A.x, B.x-A.x, A.x-P.x);
    Vec3f eq_y(C.y-A.y, B.y-A.y, A.y-P.y);
    // solve linear equation in two unknows 

    Vec3f u = eq_x^eq_y;//u,v
    if (std::abs(u.z)>1e-2) // dont forget that u.z is integer. If it is zero then triangle ABC is degenerate
        return Vec3f(1.f-(u.x+u.y)/u.z, u.y/u.z, u.x/u.z); // (1-u-v), u, v
    return Vec3f(-1,1,1); // in this case generate negative coordinates, it will be thrown away by the rasterizator
}

并且前面我们说过了，用这个重心插值算法，我们可以判断该点是否是处于三角形中，于是可以一步到位：

void fill_triangle(float *zbuffer,int x0,int y0,float z0,int x1,int y1,float z1,int x2,int y2,float z2,TGAImage &image,TGAColor color){
    // find bounding box of the triangle
    int bb_top = y0 > y1 ? (y0 > y2 ? y0 : y2) : (y1 > y2 ? y1 : y2) ;
    int bb_bottom = y0 < y1 ? (y0 < y2 ? y0 : y2) : (y1 < y2 ? y1 : y2) ;
    int bb_right = x0 > x1 ? (x0 > x2 ? x0 : x2) : (x1 > x2 ? x1 : x2) ;
    int bb_left = x0 < x1 ? (x0 < x2 ? x0 : x2) : (x1 < x2 ? x1 : x2) ;
    Vec3f P;
    for(int i=bb_left; i<=bb_right; i++){
        for(int j=bb_bottom; j<=bb_top; j++){
            Vec3f pA(x0,y0,z0);
            Vec3f pB(x1,y1,z1);
            Vec3f pC(x2,y2,z2);
            
            P.x = i;
            P.y = j;
            Vec3f bc = barycentric(pA,pB,pC,P);
            if (bc.x<0 || bc.y<0 || bc.z<0) continue;
            // if(edge_equation(x0,y0,x1,y1,x2,y2,i,j) && 
            //    edge_equation(x1,y1,x2,y2,x0,y0,i,j) &&
            //    edge_equation(x2,y2,x1,y1,x0,y0,i,j)){
            //     image.set(i, j, color);
            // }
            P.z = 0;
            P.z += pA.z*bc.x + pB.z*bc.y + pC.z*bc.z;
            
            if (zbuffer[int(P.x+P.y*width)]<P.z) {
                zbuffer[int(P.x+P.y*width)] = P.z;
                image.set(P.x, P.y, color);
            }
        }
    }
}

除此之外，这个算法还可以用来插值颜色，不过这里我们用不到。