(又过了一个多月。。)
前情提要:上一话总算是正确地把贴图之后的模型显示出来了,那么这一回要做的就是一些矩阵计算的东西了,具体的说就是使用view matrix调节相机视角,并实现perspective project,就像这样:
(加了透视投影之后,近大远小)
这一部分涉及到比较多的数学推导,原repo里解释得很细致,这里我就不再卖弄了。
https://github.com/ssloy/tinyrenderer/wiki/Lesson-4-Perspective-projection
github.com
需要了解一些的前置知识是线性代数,至少要能看懂矩阵计算,至于四元数的概念则比较抽象,如果理解了四元数这一部分掌握起来会比较快。各种缩放、旋转、平移操作如何对应到变换矩阵中,可以参照一些入门的图形学书籍。
把概念原理性的东西吃透之后,代码上的东西倒不是特别难了
首先要引入的一个新东西是Matrix这种数据类型,也就是二维矩阵,并定义好其各种运算操作。
1 | class Matrix { |
有了matrix,后面就照着公式算就行了。
其实就是图形学中的MVP矩阵变换,只不过这里只涉及P(投影)和W(视口)(注意矩阵乘法的右优先)
1 | Matrix viewport(int x, int y, int w, int h) { |
经过这一波变换之后,我们的模型已经投影到了画布上了,所以不需要再像之前一样对顶点做坐标映射。
既然到了变换矩阵这一块,那么接着往下就是MVPW里的M(Model)和V(View)
ModelView这一组合用更常见的说法就是模视变换矩阵,控制着相机以怎样的角度和方向去观察模型,当然,在我们的例子中,相机是虚拟的,我们所要做的是通过对模型进行旋转和平移,反过来体现相机视角的变化。(旋转模型和旋转相机视角其实就是互为一对逆变换的关系)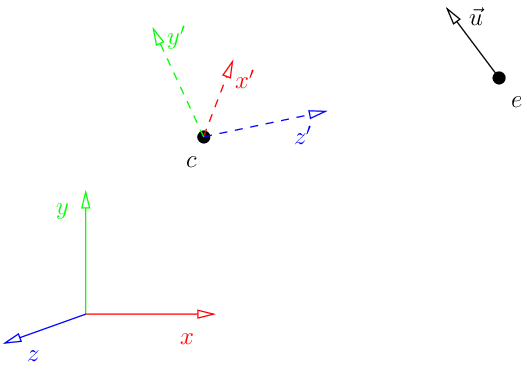
现在假设我们要实现相机在e点的效果,那么实际操作并不是移动相机而是求解原始模型的坐标系(x,y,z)到(x’,y’,z’)的一个反向变换,其中z’指向e点(有点绕,你细品)(关于相机理论,还是需要去图形学里的书里面熟悉相关概念,即相机的三个指标向量eye,at,up)
这一操作的变换矩阵的求解其实非常方便,我们已知的是z’其实就是ce向量,u是我们事先指定的相机垂直方向up,由z’叉乘u可以求得x’,进而再由z’叉乘x’求得y’。
那么代码也显而易见了:
1 | void lookat(Vec3f eye, Vec3f center, Vec3f up) { |
当然,这里与寻常的变换矩阵不同是因为这里对应的是一个反向移动。
最后,把之前的变换操作补充完整
1 | Vec3f p0_proj = m2v(ViewPort*Projection*ModelView*v2m(p0)); |
就可以得到这样的结果了:
